ANNs's Latent Representation and Concept Activation Vector

Artificial neural networks (ANNs) have become a power horse of many intelligent systems. This success is party due to its automatically way to learn representation for solving the task at hand. Consider an image classification task, previous approaches relied on hand-crafted features such as SIFT to build a program that can solve the task well. Unlike the previous approaches, artificial neural networks discover appropriate features for the task themselves through learning (i.e. optimization using backpropagation and gradient descent).

What do the latent representations of ANNs represent?

Fig. 1: Each layer learns to detect certain features. Early layers learn to detect simple features, while later layers learn to recognize complex features. Images are drawn and adapted from Lee et al. (2011).

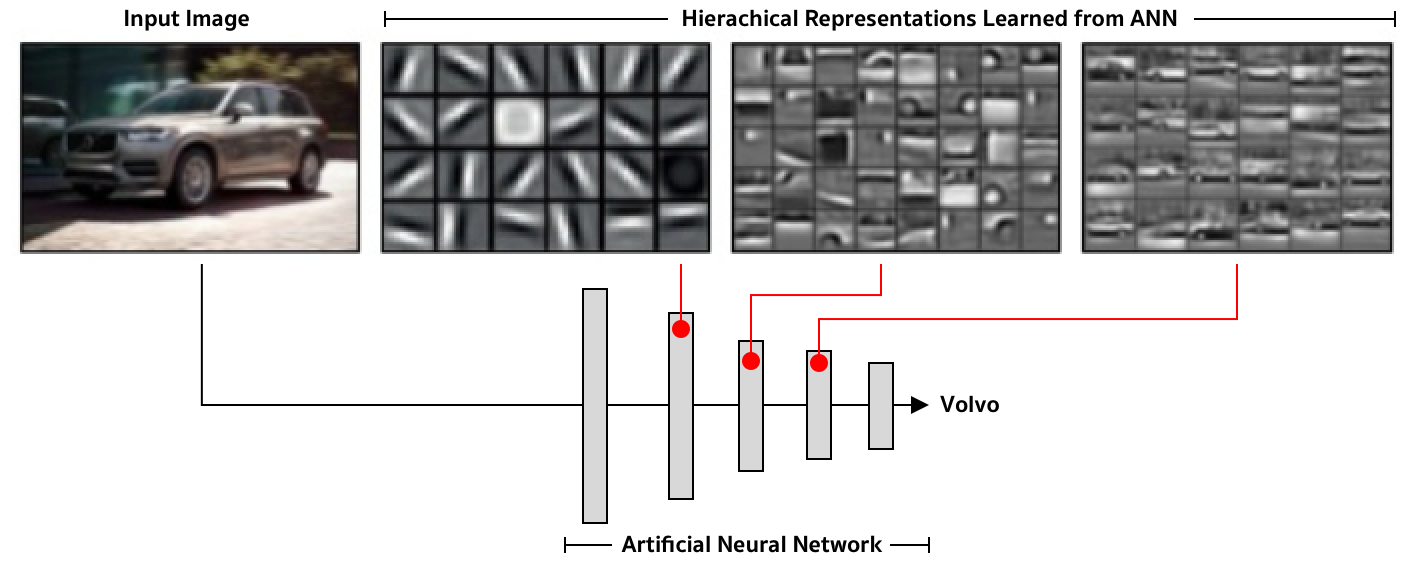
Many works have investigated what these representations of ANNs represent. For example, Lee et al. (2011) have found that early layers would learn to detect simple objects such as edges; the complexity of objects or concepts increases progressively as we move towards the last layer. In other words, the ANN learns to extract hierachical representations, progressively detacting simple to complex features. Nevertheless, it is worth noting that each coordinate of these latent space encodes certain meanings, which may or may not align with our intuition.

Another direction that we can investigate this phenomenon is to look at neightbours in these space. For example, we can use an image, take its activation at a certain layer, and then find the neighbour points (i.e. other images' activation). Most of the case, we will get these neighbour points are the images look visually to the image that we query.

Fig. 2: Finding visually similar images using latent representation from a trained ANN. More details.

Concept Activation Vector

Although there is no clear interpretation of these latent spaces, one can leverage the fact that similar samples will be close together in this spaces for building an interpretability method that can explain ANNs with human-understandable concepts.

Given a trained image classifier $f(\cdot)$, Kim et al. (2018) propose to build a linear classifier based on the latent representation $l$ of this classifier using two sets of images: one contains samples with the concept of interest and the other one is the complement (or something else). Geometrically, this linear classifier is a hyperplane in a $d$-dimension space represented by a normal vector $\mathbf v_l \in \Reals^d$, called Concept Activation Vector.

Fig. 3: Concept Activation Vector and the measure of concept alignment.

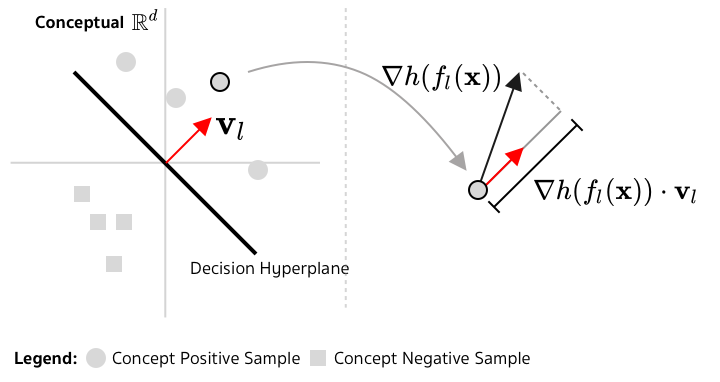
To quantify whether a certain image $\mathbf x \in \Reals^m$ aligns with a certain concept $C$, we can measure how sensitive $f(\mathbf x)$ is when the image's latent representation $f_l(\mathbf x)$ slighly moves along $\mathbf v_l$. Let denote $h(\cdot)$ the function mapping from $f_l$ to the output of $f(\cdot)$. Mathematically, this quantity is:

which is the directional derivative. If we assume that $\|\mathbf v_l \|_2 = 1$, this is the orthogonal projection of $\nabla(f_l(\mathbf x))$ on $\mathbf v_l$.

Appendix

A nice tutorial about direction derivative: KhanAcademy's Directional Derivative.